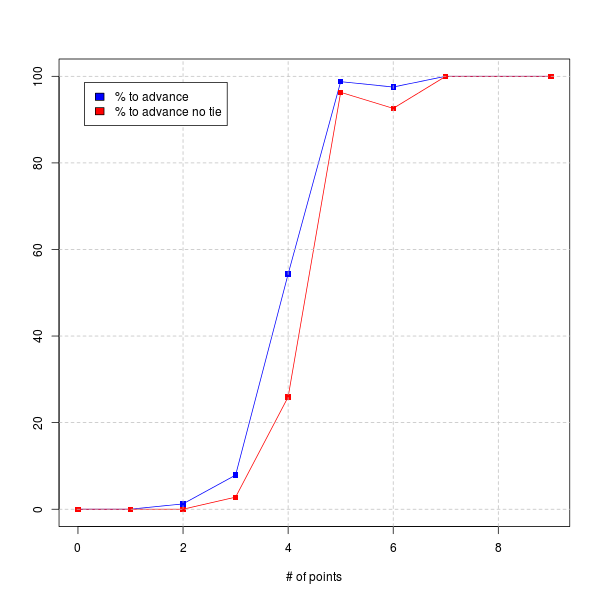
Basically, 5 points (1 win, 2 draws) means you're almost guaranteed to get out of the group, while 4 points (1 win, 1 draw) means you have around a 50-50 shot.
So...now I know! And so do you!
Tag math (33)
World Cup: how many points do you need to advance?
Mood: geeky
Posted on 2013-12-08 21:45:00
Tags: soccer math
Words: 84
After the USA was drawn into the "Group of Death", I wondered how many points the USA would need to be relatively assured of making it out of the group. So I wrote a little Python script to do the calculation, and the answer is below:

Basically, 5 points (1 win, 2 draws) means you're almost guaranteed to get out of the group, while 4 points (1 win, 1 draw) means you have around a 50-50 shot.
So...now I know! And so do you!
Falling in love by the end of this song - doing the math!
Mood: nerdy
Posted on 2013-10-26 16:19:00
Tags: math
Words: 544
But somewhere in the world someone is gonna fall in love by the end of this song,--"Odds Are" by Barenaked Ladies
Adventures in math: finding a red dot in a book, Marilyn vos Savant is wrong!
Mood: geeky
Posted on 2013-05-05 11:43:00
Tags: math
Words: 567
Let's consider the following problem, which is based on reality and caused a 15 minute argument lately: You're given a book and told it has a 90% chance of having one red dot in it (and a 10% chance of having no red dot). If you read the first half of the book and don't find a red dot, what is the probability the red dot is in the second half of the book?
To join in our argument, your choices are 90% or something less than 90%.
My stance (which I think is correct!) was that the chances go down the more you read. There are two equivalent ways to think about this:
- Assuming the location of the red dot is distributed uniformly throughout the book, before you start reading the book the chances that the red dot is in the first half of the book are 45%, in the second half 45%, and not at all is 10%. Once you know it's not in the first half of the book you can eliminate that first 45% chance, so the chances it's in the second half are (.45)/(.45+.1) = .45/.55, or around 82%.
- You can formalize this by using Bayes' theorem. Let's set up our events:
A = red dot is in book
B = red dot is not in first half of book
So the probability we want is P(A|B). (meaning the probability that A is true given that B is true)
Some values we're going to need:
P(A) = .9
P(B|A) = .5 (this is where the assumption that the distribution of the red dot is uniform comes in)
P(B|not A) = 1 (if the red dot isn't in the book, it's not in the first half!)
P(B) = P(B|A)*P(A) + P(B|not A)*P(not A)
= .5*.9 + 1*.1
= .55
So, by Bayes' theorem, P(A|B) = (P(B|A) * P(A))/(P(B)) = .5*.9/.55=.45/.55, which is the same result as we got above. You can see that Bayes' theorem is really just formalizing the logic we were using in the first case!
You can generalize this - if the red dot isn't in the first x of the book (for x between 0 and 1), then P(B|A) = 1 - x, and we end up with
((1-x)*.9)/((1-x)*.9 + .1)
So for x = 0 this is .9, as we expect (since we haven't read anything) and for x = 1 this is 0 (since we know it's not in the book). And here's the Wolfram Alpha plot of the function!
--
I was reading Parade this morning, and Marilyn Vos Savant's column had a math problem, which made me say goody! Here's the column. Unfortunately her answer is wrong. The problem with counting the combinations this way is that we're overcounting some of them. In her example, 5 is the number that you know is in the combination, and in step 1 we count the numbers 5000-5999. But then in the next step we count 0500-9599, keeping the 5 constant, and this double counts the numbers from 5500-5599. Similarly the third and fourth steps overcount, and the combination 5555 is counted four times!
The correct way to do this problem in the general case is to use the Inclusion-exclusion principle, but an even easier way is to read "at least one 5" as "everything except no 5's". So there are 10^4 total combinations, and 9^4 of them have no 5's, so the number of combinations that have at least one 5 is 10^4-9^4=3439, significantly less than 4000.
German math problem
Mood: geeky
Posted on 2010-11-20 23:39:00
Tags: math
Words: 992
As I mentioned during the Germany trip recap, visiting Allianz Arena inspired a math problem. Here it is!
Allianz Arena is home to two German soccer teams - Bayern München (hereafter "B") and TSV 1860 München (hereafter "T"). Let's assume there are 2n weeks in the season, and one game per week, and half a team's games are at home and half on the road. Presumably B and T would have to work out who gets to play at home which week, but let's say they didn't and just randomly picked which weeks they play where. What is the expected value of the number of "conflict weeks" - i.e. both B and T are scheduled to play at home?
My first step was to try this out with n=1. Then you get the following possibilities (here I just show just the weeks the team plays at home):
Week 1 TB T B
Week 2 B T TB
# conflicts 1 0 0 1
So the expected value of the number of conflicts is .5 for n=1.
Now, I took a guess at what the expected value was in general. As a rough guess, each team has to choose n weeks, so you might expected about half of them to overlap. But it seemed to me that once you do have a conflict week, the chances of another one would go down (since you've "used up" one game from both teams), so I thought it might be a bit less than n/2.
So - onwards to discovering the answer! It seemed fairly easy to write this out as a recurrence relation with the following parameters:
c(w,b,t) = expected number of conflict weeks if there are w weeks in the season, b home games for B left, t home games for T left.
Base cases: c(w,b,0) = c(w,0,t) = 0 [no games left for one team means no conflicts]
c(w,w,t) = t and c(w,b,w) = b [if one team has to play all their games in the remaining weeks, however many the other team has left is the number of conflicts]
And we write the induction step by looking at the first week:
c(w,b,t) for 0 < b,t < w is:
(w-b)/w * (w-t)/w * c(w-1,b,t) [chance that b and t don't play a game this week times what happens for the rest of the season]
+ b/w * (w-t)/w * c(w-1,b-1,t) [chance b plays a game this week and t doesn't]
+ (w-b)/w * t/w * c(w-1,b,t-1) [chance t plays a game this week and b doesn't]
+ b/w * t/w * (1 + c(w-1,b-1,t-1)) [chance both play a game this week, so the expected value goes up by 1]
This looked correct, but was a little discouraging because it seemed very not obvious what an explicit formula would be. But it was easy enough to code a quick Python script to get a hint to what an answer would be.
The results were highly suggestive: c(2,1,1) = .5 (this is the case we worked out by hand above), c(4,2,2) = 1, c(6,3,3) = 1.5, c(8,4,4) = 2, c(10,5,5) = 2.5, etc. So it sure looked like c(2n,n,n)=n/2.
But I really wanted to prove it, but dealing with this kinda ugly recurrence relation didn't seem like the way to go. Also, this seemed like a combinatorial problem and it seemed like there should be a nice combinatorial way to express c(2n,n,n).
After some thought I came up with a good way of thinking about it. Let's say without loss of generality that B's home games are the first n of the season. Then you're just choosing T's home games and seeing how many overlap with the first n. This leads fairly naturally to the explicit formula:
c(2n,n,n) = (sum_{i=0}^n [(n choose i) * (n choose (n-i)) * i])/(2n choose n)
Here i represents the number of conflicts, and the chance of getting that many conflicts is the same as choosing i games in the first n weeks of the season (which will be conflicts), and the remaining n-i in the second n weeks of the season. In total, you're choosing n weeks out of 2n, which is where we get the denominator from.
This didn't seem like a huge improvement at first, but we can actually simplify this a lot. First of all, (n choose i) = (n choose (n-i)), so we get
c(2n,n,n) = (sum_{i=0}^n [(n choose i)^2 * i])/(2n choose n)
Now, notice that (sum_{i=0}^n [(n choose i)^2]) = (2n choose n)). The right side is the number of ways of counting choosing n objects out of 2n choices, and the left side is the same - first you choose which i are in the first half, and then which (n-i) are in the second half (since (n choose i)=(n choose (n-i)). So this will help out in a minute.
Now let's consider two cases:
Case 1: n is odd, i.e. n=2k+1 for some integer k.
Let's just look at the numerator of c(2n,n,n) and split it up in half to get
sum_{i=0}^k [(n choose i)^2 * i] + sum_{j=k+1}^n [(n choose j)^2 * j]
Here we can pair up i's and j's that sum to n - since 0+n=n and k+(k+1)=2k+1=n, this covers all of them. Since i+j=n, then (n choose i)=(n choose j), so we'll end up with
sum_{i=0}^k [(n choose i)^2 * i + (n choose i)^2 * (n-i)], or
sum_{i=0}^k [(n choose i)^2 * n]
Now we can unsplit this back into the i's and j's, giving n/2 to each side to get
sum_{i=0}^k [(n choose i)^2 * (n/2)] + sum_{j=k+1}^n [(n choose j)^2 * (n/2)]
which simplifies down to
sum_{i=0}^n [(n choose i)^2 * (n/2)]
(n/2) * sum_{i=0}^n [(n choose i)^2]
Since we showed above that this sum is equal to (2n choose n), this means that
c(2n,n,n) = ((n/2) * (2n choose n))/(2n choose n) = n/2, as desired!
Case 2: n is even, i.e. n=2k for some integer k.
This is the same as the previous case, except we have the additional value i=k which doesn't pair up with anything. But, the value that we're summing for i=k is ((n choose k)^2 * k) and k does equal n/2, so it reduces the same way!
In short, I love combinatorics!
Who really won the World Cup?
Mood: geeky
Posted on 2010-07-11 16:22:00
Tags: soccer math
Words: 579
Congrats to Spain, although the final game was not super impressive.
Anyway, before the World Cup, I bought an ESPN magazine guide. It included "measures of success" for all 32 teams, so I thought it would be fun to see who did the best relative to their predictions.
Key:
HH = Happy to be Here = 0 points
OG = Out of Group stage = 1 point
QF = QuarterFinal = 2 points
SF = SemiFinal = 3 points
F = Final = 4 points
W = Win it all = 5 points
(note that the score = 5 - log_2(# of teams left at that stage))
So, without further adieu: (mouseover flag for country name)
| Group | Success | Actual | Difference | |
|---|---|---|---|---|
 | E | SF | F | +1 |
 | A | QF | SF | +1 |
 | F | OG | QF | +1 |
 | E | HH | OG | +1 |
 | F | HH | OG | +1 |
 | H | W | W | 0 |
 | D | SF | SF | 0 |
 | D | QF | QF | 0 |
 | H | OG | OG | 0 |
 | B | OG | OG | 0 |
 | C | OG | OG | 0 |
 | B | HH | HH | 0 |
 | H | HH | HH | 0 |
 | F | HH | HH | 0 |
 | G | HH | HH | 0 |
 | C | HH | HH | 0 |
 | C | OG | HH | -1 |
 | E | OG | HH | -1 |
 | A | OG | HH | -1 |
 | D | OG | HH | -1 |
 | H | OG | HH | -1 |
 | C | SF | OG | -2 |
 | A | SF | OG | -2 |
 | G | SF | OG | -2 |
 | D | QF | HH | -2 |
 | E | QF | HH | -2 |
 | A | QF | HH | -2 |
 | B | QF | HH | -2 |
 | B | W | QF | -3 |
 | G | W | QF | -3 |
 | F | SF | HH | -3 |
 | G | SF | HH | -3 |
| Group | Total success | Total actual | Difference |
|---|---|---|---|
| E | 6 | 5 | -1 |
| F | 4 | 3 | -1 |
| D | 8 | 6 | -2 |
| H | 7 | 5 | -2 |
| C | 5 | 2 | -3 |
| A | 8 | 4 | -4 |
| B | 8 | 3 | -5 |
| G | 11 | 3 | -8 |
| Total | 57 | 31 | -26 |
| Continent | # of teams | Total success (avg) | Total actual (avg) | Difference (avg) |
|---|---|---|---|---|
| Asia/Australia | 5 | 3 (0.60) | 2 (0.40) | -1 (-0.20) |
| North America | 3 | 4 (1.33) | 2 (0.67) | -2 (-0.67) |
| Europe | 13 | 25 (1.92) | 15 (1.15) | -10 (-0.77) |
| South America | 5 | 14 (2.80) | 10 (2.00) | -4 (-0.80) |
| Africa | 6 | 11 (1.83) | 2 (0.33) | -9 (-0.81) |
home energy usage vs. temperature
Mood: geeky
Posted on 2009-11-09 12:48:00
Tags: math projects
Words: 62
I couldn't sleep last night so I whipped up this analysis of our home energy usage vs. temperature. It turns out that (spoiler!) we use more energy when it's hot outside. But I got to run my first linear regression!
People who know about statistics: feel free to criticize/suggest improvements. (I'm not even sure I was looking at the right R-squared value...)
A week of happy recap, and ismydatasignificant.com
Mood: okay
Posted on 2008-12-19 10:50:00
Tags: health math projects happiness
Words: 307
So I started the week of happy a week or so ago, and I'm pretty...happy with the results. It turned out to be kind of a tough week, what with the root canal and the painful aftermath, but focusing on the little things that make you happy during the day is good. I'm pretty sure I read somewhere that big changes in lifestyle (new bigger house, etc.) don't generally affect one's happiness level in the long run, but little things can if you focus on them. Or something like that.
Dentistry - I gave in and called this morning to make sure it was normal for the pain to last all week. The person I talked to told me to come in, and they took an X-ray and thank goodness everything looks fine. (if I had had to have like another root canal or something I would have been seriously sad) She said the pain can last a while, and as long as it's getting better (it is!) it's OK, and she gave me another prescription for Zipac(sp?) to take in case there's a lingering infection or something. (and she told me to switch to Advil instead of Tylenol for the inflammation) So, yayish!
Last night when I got home quijax was watching Mythbusters, which I don't get to see much but I like! One of the myths they were busting was that buttered toast tends to land buttered side down, and long story short they ended up dropping toast off of a building and observing. Anyway, the results were slightly more in favor of the toast landing buttered side up, and Jamie had a physics explanation (when you butter toast it gets indented) but their numbers weren't convincing. Long story short, I created ismydatasignificant.com for an easy chi-squared test for significance. If only I understood more statistics...
"I wish I had done this!"
Mood: geeky
Posted on 2008-11-26 10:16:00
Tags: essay math programming links
Words: 387
"I wish I had done this!" is my highest praise for a website. The last time I can remember using it was for wowjutsu, which tracks raid progression in WoW by looking up what gear people are wearing in the Armory and matching that with where that gear came from. Simple idea, useful, interesting, but the technology behind it is something I totally could have done.
My newest "I wish I had done this!" is StateStats. You enter a search term, it finds which states in the US search for that term more per capita, then gives you a nice heat map of the US. But then it correlates that with a host of other state rankings: obesity, income, high school graduation rates, voted for bush, percent youth, etc., etc., etc. So you can see that searches for "prius" are correlated with income and negatively correlated with energy consumption. Or searches for "gay" are correlated with density (i.e. more urban states) and negatively correlated with voted for bush. Or searches for "lsu" are highly correlated with, well, being Louisiana. Or searches for "coke" are highly correlated with obesity, while searches for "soda" are highly negatively correlated with obesity. (huh?) Or searches for "tea" are correlated with income and negatively correlated with voted for bush.
Anyway, it's a ton of fun to play with, and the example queries ("garth brooks" is highly correlated with voted for bush!) are interesting, but it's even more fun to think of a common search term and see what pops up.
The correlation metric it's using is just based on rank and not intensity - i.e. it's just the order of the 50 states that matter, not how much the first place one is bigger than the second place one. This probably leads to some false positives when the numbers are very close together. Also, I'd imagine there's a natural inaccuracy determining which state a particular query is coming from, and since you're looking at things only on a state by state level (as opposed to county by county or something) it's not as precise as it theoretically could be.
And don't forget correlation is not causation - searching for "hockey" does not make it colder outside, or make you richer.
I award StateStats the official "I wish I had done this!" seal of approval.
link monday
Mood: blah
Music: Smashing Pumpkins - "The Beginning Is The End Is The Beginning"
Posted on 2008-11-24 10:31:00
Tags: netflixprize math links
Words: 364
I'm actually feeling a bit down from finishing my talk - I guess I was looking forward to it more than I thought? It's weird. Maybe I need to work on whereslunch.org some more or something. Anyway, to cheer myself up:
talk went well!
Mood: chipper
Posted on 2008-11-22 12:58:00
Tags: math
Words: 38
The talk went well! The kids seemed to understand, and in some cases jumped the gun on stuff (which is fine). Here's the talk in ppt format (and in odp format) and the worksheet in pdf format.
Yay!
is it Saturday yet?
Mood: busy
Posted on 2008-11-19 12:54:00
Tags: math links
Words: 175
Saturday is my math talk; last night I finished the slides and wrote up a worksheet. Things look pretty good - tonight I plan to do a trial runthrough and make some changes to the worksheet. (I'll post all this stuff when it's done for posterity's sake...) At this point, I've spent probably 8 hours preparing for my 1.5 hour talk (which includes the students working on the worksheet) and I expect that'll rise to 10 hours of preparation by the time this is over. How do you teachers do it? This is crazy. I'm really looking forward to having my evenings back...(not that it isn't kinda fun preparing, but it's getting a little old)
Making some progress on my annoying bug at work. No longer freaked out about teeth. The week is looking up!
A long look at the people who saw the subprime mortgage crisis coming, written by Michael Lewis.
Five Physics Lessons for Obama - good stuff in here. I think nuclear power is a pretty good way to go, assuming it's managed well.
life recap
Mood: busy
Posted on 2008-11-17 09:51:00
Tags: 23andme math wedding worldofwarcraft genetics
Words: 504
World of Warcraft:
The second expansion to WoW, called "Wrath of the Lich King" (or WotLK) released Wednesday midnight. (the late midnight, not the early midnight)
We assumed it was like other midnight release events we had been to - get in a short line to pay and get your receipt validated (sticker or highlighter squiggle or whatever), then wait in a longer line to get the game (that would only start moving at midnight). We walked by the tent where there was some music and stuff, and decided to wait in line to pay first before enjoying the festivities.
It turns out, there was only one very long line, and that was the line to pay. So we gamely got in the back and waited in the cold (djedi ran in to Barnes & Noble and got me a hot chocolate and himself a tea :-) ). And waited. And waited. Every fifteen minutes or so we'd move up like four or five paces. I wish I was exaggerating. wildrice13 and later destroyerj joined us so that was kinda fun, but midnight came and went and we were still in line. At this point the smart thing to do probably would have been to give up and come back the next morning (especially since I had to get up early to take destroyerj and skimmerduk to the airport) but that never occurred to me. Finally at 2:20 we got our copies and left. They only had two registers going for what must have been 500 people. Booo gamestop!
Having said that, the game is good and I got it to install on linux with the usual tweaking.
Math talk:
My math circle talk is Saturday, and it's coming along OK. I finished sketching out the talk and worked on my slides last night, although I then changed part of the talk to make a bit more sense. New theme: graph theory in computer science, with parts about register allocation and Huffman encoding. Still need to actually do the rest of the slides, then make up a worksheet, then practice it. I did get to pick out what sort of cookies would be served, though, so that's a plus :-)
Game night:
Sorry to those who I told we'd be hosting a game night this week, but between talk preparation stuff and djedi work crunch time we can't do it this week. Hopefully soon, though.
23andMe:
I think I'm going to take the plunge and get my DNA analyzed soon, maybe after the talk. Should be fun and exciting!
Wedding/Commitment ceremony planning:
We're actually starting to move forward on this - investigating locations, etc. More stress to come, I'm sure.
what's on my mind
Mood: okay
Posted on 2008-11-11 10:11:00
Tags: whereslunch math projects
Words: 209
graph colorings and network flows
Mood: concerned
Posted on 2008-11-08 19:43:00
Tags: math
Words: 164
I agreed to give a talk to the Austin Math Circle in a few weeks, so today I tried to figure out what it should be about. I think I'm going to talk about graph theoryish things - the way things work, I'll be talking for a while, then the kids will work on part of a worksheet, then a break for cookies and stuff (I love cookies!), then more talking and more of a worksheet. First part will be on coloring (hoping to prove the six-color theorem) which I've got pretty well sketched out. (although I need slides too! ack...) Second part is less clear - I think something on network flows would be interesting, but I'm not sure I can come up with enough material that isn't too complicated and I can explain well. I guess I'll work on that tomorrow.
(also, this is the first post I've made in...man, maybe two months? in which I didn't mention the election, this postscript notwithstanding. Hooray!)
target probabilities - done!
Mood: proud
Posted on 2008-06-04 08:59:00
Tags: math projects
Words: 32
Check it out! Or, if you're in a hurry, at least check out the awesome graph! (I spent a while coming up with a decent algorithm for label placement...)
Onward to...something else!
people like talking to people they don't like
Mood: awake
Posted on 2008-06-02 13:04:00
Tags: math projects politics
Words: 165
According to a new Gallup poll, 67% of Americans believe the president should meet with the leaders of enemy countries, and 59% of Americans believe the president should meet with the president of Iran. (I guess that means 8% of Americans don't think Iran is an enemy?) That seems like a pretty firm rebuttal of McCain's attacks on Obama for wanting to do just that.
The Target probability page is really filling out now. I think I'm going to give up on justifying the counts for a mixed straight (a 4 card straight including cards of all 4 suits) which seems really really tough to count, and maybe the 3 card and 4 card straight flush of any suit (which are only really tough to count, but still more than I'm up for). After I calculate the numbers I'll do a graph and try to figure out what the dividing line is of which targets are worth which points, and see if any are "misclassified".
an early midlife crisis?
Mood: busy
Posted on 2008-05-27 12:41:00
Tags: whereslunch essay xkcd math projects
Words: 159
Lately I've been feeling a lack of...something. A desire to build something great, some awesome website or something. I don't know where it's coming from and maybe it'll just fade away. Drive isn't bad, but it's kinda inconvenient. I just don't have a whole lot of time to devote to stuff like that.
Although, keep your eyes open for whereslunch.org after I finish my current project!
Speaking of which, last night in bed I finally figured out how to use inclusion-exclusion to calculate the number of 3 card straights, etc. The key is to make your sets "hands that don't include a green 0", "hands that don't include a green 1", etc., figure out the number of hands in the union of those sets and then take the complement. I guess it's been a while since I've done this combinatorics stuff. I also filled out some more entries in the table with explanations.
xkcd story in the NY Times!
mathing it up after dark
Mood: cheerful
Posted on 2008-05-20 09:37:00
Tags: music math projects
Words: 218
I couldn't sleep last night, so I worked on the Target probabilities project. It was annoying me that the old version of the generated HTML (which was generated by LaTeX2HTML) looked kinda ugly - look how jagged the math graphics are! (especially compared with the beauty that is the generated .dvi file) So I tried a few different packages and settled on TeX4ht, which produced this much nicer looking page. Ah, that's better. (although why is that table floating to the right? grr)
I've been making slow progress on actually figuring out the numbers (3 card straights and straight flushes are the worst!) but I'm getting there. Getting the right numbers is a little more challenging.
Before that, we watched Citizen Kane (still good even though we weren't paying full attention) and I played some GTA IV, including a little multiplayer with destroyerj. It was tough without a headset and sucking at the game :-) I managed to flip the cop car we were driving in, and another time destroyerj was driving and I was shooting at something and I saw him jump out of the car. Had just enough time to wonder "Huh?" before we slammed into a stopped car and caught on fire :-)
Finally downloaded The Slip by Nine Inch Nails. So far: very good.
Game night tonight!
post-WoW doldrums
Mood: excited
Posted on 2008-05-13 10:09:00
Tags: math projects worldofwarcraft
Words: 147
seem nonexistent. (anyone know a good antonym for "doldrums"?) Last night we bought some exciting new books, I bought GTA IV, got a graduation present for my sister, and committed to working on my new project. (calculating the probability of satisfying target cards in the game of Target)
It seems that my computer is under attack from a botnet. I pretty frequently get ssh requests coming from wildly different IP addresses trying out a dictionary list of user names. I'm not too worried about them guessing a username/password combo but the fact that they're hitting my box in general is a little scary. I've started turning off ssh at night but I do use it occasionally during the day...
things younger than mccain
If you're in to electoral predictions (for the general election), fivethirtyeight.com is a godsend. Probabilities that each candidate will win each state, cartograms, graphs...
Theorycrafting: upgrades from Zul'Aman
Mood: nerdy
Posted on 2008-04-18 16:48:00
Tags: math theorycraft worldofwarcraft
Words: 161
Since I revamped the Frost mage DPS calculator to include Icy Veins and the Water Elemental, plus the fact that Zul'Aman is almost on farm status for us, time to look at what upgrades I would like!
For me right now, 1 point of sustained DPS = 13 int = 3.6 spell crit = 1.9 spell haste = 1.75 +damage = 1.45 +spell hit (still not capped out!)
| Gear | DPS vs lvl 73 (boss)/DPS vs lvl 70 |
|---|---|
| Current | 888.8/925.9 |
| Footpads of Madness | 901.5/939.0 |
| Wub's Cursed Hexblade | 888.7/927.2 |
| Hood of Hexing | 917.1/933.3 |
| Loop of Cursed Bones | 898.5/942.4 |
| Mantle of Ill Intent | 904.0/941.6 |
| Shadowcaster's Drape | 899.0/936.5 |
| Mana Attuned Band | 912.0/937.1 |
number of Blokus games?
Mood: awake
Posted on 2008-02-28 13:50:00
Tags: math
Words: 253
Last night we were playing Blokus and I wondered how many possible games of Blokus there were. Todd said it shouldn't be too hard to figure out, so I'm gonna start working on a script to calculate it. I'm assuming the colors all start in a fixed corner and normal rules apply (except you have to play a piece if you can), and I'm counting the number of games and not the number of board positions because it seems easier.
How many possible games do you think there are? For reference, there are somewhere around 1014 legal board positions in Connect 4, 1050 board positions in Chess and 10171 board positions in 19x19 Go (from this Wikipedia article, which unfortunately doesn't list the number of games) I'm going to guess something like 1080 which, come to think of it, means it might not be possible to count them all in a reasonable length of time. Still, worth a shot!
Thousands of people might be infected with Hepatitis C or HIV in Las Vegas. From the article,
The virus may have been spread when clinic staff reused syringes and used a single dose of anesthesia medication on multiple patients, the district said.Now maybe my perspective is different because my mom's in public health, but a clinic sharing syringes?? How could this happen?
To retain its state license and Medicare certification, the center faces increased on-site inspections and fines yet to be determined.Yeah, this is a pretty big screwup.
houses houses houses...I made you out of clay...
Mood: creative
Posted on 2007-12-21 10:22:00
Tags: math elevator work house poll
Words: 408
We went house-hunting again yesterday. The first house we looked at is now our current favorite (which is good, as we heard our previous favorite is already under contract. Stop buying houses, people!), with a nice big kitchen (with an island!) that opens up to a living room which is a little on the small side but could probably fit the TV and computers. Master bedroom is plenty big and the bathrooms are nice. Plus it was built in the 90s and is reasonably priced!
Downsides:
- a bit far from freeways, although the neighborhood it's in is nice (it's off of Duval)
- there's a deck in the backyard which would be nice were it not so rundown, presumably by the current owners' (don't yell at me, there's more than one owner so I'm assuming they both own the dogs) dogs.
- living room is a little small
We have another good possibility that we'll see after the holidays, hopefully.
Now for the important stuff: at work my building has 8 floors and elevators. I work on the 8th floor, so I get plenty of time in said elevators. (fun thing to do: walk in a circle as the elevator is moving and realize that you're tracing out a helix!) Often I have to wait for other people to get off on their stupid less important floors before I get to the top, so I was wondering: let's say it's a given that we have to make two floor stops from 1 to 8. Is it better to have the stops be consecutive or spread out? For the sake of concreteness, let's say one way we stop at floors 2 and 3, and the other way we stop at floors 3 and 6.
I have an idea but I'll cut it:
Anyway, I was going to start taking measurements when I get my new phone, but it looks like the RAZR V3 doesn't have a stopwatch. (can anyone confirm?) That makes me sad. I'll come up with something, though!
arena rating graph
Mood: bouncy
Posted on 2007-11-09 14:51:00
Tags: netflixprize math projects worldofwarcraft
Words: 234
Went out to lunch today with WoW people and we talked about this neat idea for an Arena rating graph. So you start at a 1500 rating and every match you play you gain or lose 1-29 points, and it would be neat to see the progression of that as the season goes on. Also nice to see what composition of teams we're good against and which we're not, and the ratings of the teams we win or lose to. I'm having to try really hard not to just start writing down ideas here since it's not work-related :-)
My first thought was to do the graph in Flex, but I forgot that Flex Charting is a separate package that costs money. So I did some research and there are lots of options for this sort of thing (found this excellent article on interactive charts and graphs via del.icio.us). AmCharts looks like the best option, with FusionCharts Free close behind. I'll have to download and try them out at home; of course the hard part will be figuring out how to display all that data in a useful way.
Here's an excellent article on how Simon Fink's team got into the top 10 for the Netflix Prize - lots of juicy juicy math. Makes me want to get back into that sort of thing, which would make three active projects at once, which is too much.
Theorycrafting: upgrades from Kara
Mood: excited
Posted on 2007-10-18 11:31:00
Tags: math theorycraft worldofwarcraft
Words: 181
Since my last set of calculations, I've gotten a lot of upgrades, and so I'm wondering what's left out of Kara that I want. Here's an updated list (including all gear from Kara since it's basically on farm status), using my mage DPS calculator:
| Gear | DPS vs lvl 73(boss)/DPS vs lvl 70 |
|---|---|
| Current | 685.8/701.4 |
| Brooch of Unquenchable Fury (Moroes) | 688.3/700.6 |
| Shadow-Cloak of Dalaran (Moroes) | 687.7/703.4 |
| Nethershard Girdle (Moroes) | 681.1/706.5 |
| Staff of Infinite Mysteries (Curator) | 694.1/717.0 |
| Malefic Girdle (Illhoof) | 686.2/711.8 |
| The Lightning Capacitor (Illhoof) | someday I'll figure it out |
| Tirisfal Wand of Ascendancy (Shade) | 691.5/701.0 |
| Adornment of Stolen Souls (Prince) | 685.6/706.5 |
| Nathrezim Mindblade (Prince) | 715.0/739.8 |
| Ruby Drape of the Mysticant (Prince) | 695.4/700.9 |
Theorycrafting: calculating my DPS
Mood: geeky
Posted on 2007-09-13 10:00:00
Tags: math theorycraft worldofwarcraft
Words: 220
So I whipped up a little DPS calculator which is unfortunately specific to my talent build. Anyway, it's fun to play with. (for me; results may vary if you're someone else) My current numbers are +644 frost dmg, +598 fire dmg, 524 intellect, 222 crit rating, 83 hit rating. This gives me DPS on my frostbolt/fireblast/total as 621/675/630. For fun, what happens if I replace my gear with gear from Kara? (assuming I get all the same enchants)
| Gear | frostbolt/fireblast/total DPS |
|---|---|
| Current | 621/675/630 |
| Harbringer Bands | 622/675/631 |
| Handwraps of Flowing Thought | 619/687/630 |
| Brooch of Unquenchable Fury | 624/678/633 |
| Nethershard Girdle | 617/668/626 |
| Shadow-Cloak of Dalaran | 624/676/632 |
| Bands of Nefarious Deeds | 625/677/634 |
| Gloves of the Aldor (T4) | 620/687/632 |
| Staff of Infinite Mysteries | 639/688/647 |
| Malefic Girdle | 622/671/631 |
| The Lightning Capacitor | hahaha I have no idea |
| Tirisfal Wand of Ascendancy | 626/680/635 |
| Jewel of Infinite Possibilities | 630/685/639 |
| Uni-Mind Headdress | 636/688/644 |
Theorycrafting: spell hit rating and me
Mood: geeky
Posted on 2007-09-12 15:48:00
Tags: math theorycraft worldofwarcraft
Words: 352
Last night some gear dropped in Kara and I was next on the unofficial Suicide Kings list for loot and I couldn't decide whether to take it or not because of stupid spell hit rating. So I'm going to work out how much spell hit rating is useful for me in the hope of avoiding this in the future. This is all based on the Spell hit article in WoWWiki.
For raiding, bosses are considered to be level 73, which means by default I have a 83% chance to hit them with spells. I have 3/3 points in Elemental Precision which gives me +3% hit for Frost and Fire spells (which is all I ever cast on bosses), bringing me to 86%. The maximum hit chance possible is 99%, so that leaves a 13% gap.
1% of spell hit chance is the same as 12.6 points of spell hit at level 70, so that means I need 13*12.6=163.8 spell hit rating to max out. Since I have 5/5 points in Ice Shards, my frost spells crit bonus is 100%. Unlike melee attacks, for spells hit and crit are separate rolls. So 1% of spell crit chance is really worth (chance to hit)%. So spell hit does more good than spell crit. (for fire spells spell hit is even better, since by default the crit bonus is only 50%) It takes 22.1 spell crit rating to get 1% of spell crit chance at level 70.
Summary: I only have 83 spell hit rating with my current gear, so I need another 80 spell hit rating to max that out. When comparing gear, since my current spell hit chance is 92.6%, 1 point of spell hit is worth around (22.1/12.6)/(.926)=1.9 points of spell crit, and this is underestimating spell hit since I do cast fire spells in my normal rotation (frostbolt, frostbolt, fire blast, ...) Also, spell hit is worthless on my PvP gear since my chance to hit is 96%+3%=99% on lvl 70 opponents, which is maxed out.
Next time, how much spell hit/crit is worth versus +spell damage!
Thanks to destroyerj for corrections.
Haskell wearing me down
Mood: worried
Posted on 2007-08-15 10:57:00
Tags: math haskell projects
Words: 344
but first, math!
From last time - the answer is that they're not symmetric. If a=10, b=11, c=20, then C enters A's stall at time 10 and you get to enter B's stall at time 11. However, if a=20, b=11, c=10, then C enters B's stall at time 11 and you have to hold it until time 20. More formally, the time you have to wait is
min(min(a,b) + c, max(a,b))
Using the formulas min(a,b) = (a+b-|a-b|)/2 and max(a,b) = (a+b+|a-b|)/2, this expression simplifies down to (a+b+c-|c-|a-b||)/2, which is clearly not symmetric in a and c. I'd be interested to see how this formula works for more people and stalls - it seems to blow up pretty quickly, although it would be easy to write a program to calculate it. I have a gut feeling that you want the fastest people earlier in the line (ideally if there are n stalls the n-1 slowest people will be all in their stalls when you get to go in, so you don't have to wait for them) but proving that seems rather tricky.
When will LJ get inline LaTeX?? :-)
Good article about risk management and terrorism (via schneier)
I'm making good progress rewriting the Pretty Pictures picture generator in Haskell - it spits out valid PPM images that look correct for simple cases, but it needs more testing. (and I need to see if browsers support PPM natively or if I have to convert to PNG which would be a pain) I'm not enjoying it a whole lot, though. The idea of learning Haskell was to expand my mind and change the way I programmed, and I guess it has done that some, but I always feel handcuffed when I sit down and try to do seemingly easy things, like write out a raw PNG file. (got about halfway there and said forget it)
To antidote this (yes, it's a verb!) I think my next project will be less challenging technically and more interesting, like involving lots of neat data (census? past wars?) and some sort of neat visualization. (R?) We'll see.
weekend at bengies
Mood: pessimistic
Posted on 2007-08-13 10:32:00
Tags: math
Words: 336
Does anyone know why the I-95 tunnel under Baltimore Harbor is a tunnel and not a bridge? Is it cheaper or something? Hmm, according to Wikipedia:
Neat!
Original plans called for an eight-lane bridge across the Baltimore Harbor to complete the final segment of Interstate 95 in Maryland. However, it was determined that a bridge would have had a negative environmental and aesthetic impact on the nearby National Monument and Historic Site at Fort McHenry and the neighboring residential communities of Locust Point and Fells Point.
math and dodgeball
Mood: cheerful
Posted on 2007-01-20 12:59:00
Tags: dodgeball math
Words: 358
As I was laying in bed last night, I realized that there was a simplification for the sum in yesterday's post. So the number of possible auctions we calculated to be 1 + 28 * sum from i=1 to 35 of (35 C i)*21^(i-1). Let's look at sum from i=1 to 35 of (35 C i)*21^(i-1) = (1/21) * sum from i=1 to 35 of (35 C i)*21^i = (1/21) * [(sum from i=0 to 35 of (35 C i)*21^i) - 1]. (this will make our argument easier)
So what is sum from i=0 to 35 of (35 C i)*21^i? We can use a combinatorial argument (counting the same thing two different ways) to simplify this. Let's say we have 35 slots, and for each slot we have a choice of the numbers 0 through 21 (inclusive). One way to count this is that we have 22 choices for each slot, and since there are 35 slots, there are 22^35 configurations. Another way to count this is to first choose how many slots will contain the number 0 - let's say there are i such slots. Well, we have (35 C i) ways to choose which slots have 0, and then there are 21 choices (since 0 isn't a possibility) for the other (35-i) slots, so this gives (35 C i)*21^(35-i). Since i can be anything from 0 to 35, there are in total sum from i=0 to 35 of (35 C i)*21^(35-i) configurations. Now, if we let j=35-i, this is the same as the sum from j=0 to 35 of (35 C (35-j))*21^j (since j will range from 0 to 35 just like i did), which is equal to the sum from j=0 to 35 of (35 C j)*21^j. This is just what we wanted!
So we have shown that the sum from j=0 to 35 of (35 C j)*21^j=22^35. Plugging this back in to our expression for the number of possible auctions, we get 1 + 28 * [(1/21) * (22^35 - 1)], which is in fact 128745650347030683120231926111609371363122697557 as desired. So I didn't have to do that ugly sum after all :-)
Dodgeball was rough - we lost 10-1 and 13 or 14-0. No major injuries, though, so that's something!
Friday bridge math puzzle!
Mood: tired
Posted on 2007-01-19 08:19:00
Tags: bridge math
Words: 763
onefishclappin forwarded me this fascinating puzzle yesterday, and I thought "Ooh, I should figure this out", then started thinking about it, then went back to work for about 5 seconds, then gave up and worked it out (roughly). Here it is:
After you've dealt out a hand, are there more different legal ways to play out the hand, or more ways to bid the hand?
Here, only legal plays and bids are counted, so no bids or plays out of turn, insufficient bids, revokes, etc. Other than that, the plays or bids don't have to make any particular bridge sense, they just have to be legal.
The wonderful game called Tsuro
Mood: okay
Posted on 2007-01-05 23:39:00
Tags: math
Words: 794
One of the things I did over break was play a beautiful game called Tsuro. It's a quick (20 minutes or so) game that supports up to 8 people (it's actually better with 8 people!) with simple rules. And it's a thing of beauty, both in artwork and elegant design.
The board is a 6x6 grid that tiles are placed on. It starts empty. The tiles take the following form:
1 2
---+---+---
| |
| |
8 + + 3
| |
| |
7 + + 4
| |
| |
---+---+---
6 5
where the numbers 1-8 label the points on each tile. Each point on a tile is connected via a path to exactly one other tile, so a tile that had 1 connected to 8, 2 to 6, 3 to 4 and 5 to 7 would look something like:
1 2
---+---+---
| | | |
| / | |
8 +- / /+ 3
| | | |
| / | |
7 +-- | \+ 4
| \-+- |
| / \ |
---+---+---
6 5
except a whole lot prettier.
Now, every player has a piece which starts on the outside of the board, lining up with the 2 pieces per tile edge rule. You have a hand of tiles, and on your turn you play a tile on a space your piece touches. You then move all pieces that touch that on the paths the tile indicates, so if your piece started on the 6 point it would move to the 2 point. Of course, if your piece then ends up touching a tile that exists, your piece follows the paths on that tile, and so on. The goal is to survive; your piece dies if it goes off the board, and both pieces die if there is a head-on collision of pieces.
The neat part is that there are exactly 35 tiles, enough to fill up the 6x6 grid save one empty square. In order to survive the game, your piece must end up touching that empty square. It's an elegant end condition.
But it gets even better. I wondered how many different tiles there could possibly be, excluding rotations of the same tile. (since you can rotate them when you play them) If the answer was in fact 35, that each distinct tile was used exactly once and that just happened to work out to be 6^2-1 that would be proof that this game was, in fact, given to us mere mortals from the heavens.
Let's not get ahead of ourselves, though. Firstly, how many tiles are there without caring about rotations? The way I came up with counting it is to first arrange 1-8 in a row - there are 8! ways to do this. Now pair up each consecutive number, so if we had the string 46231785, that would pair 4 and 6, 2 and 3, 1 and 7, and 8 and 5. However, we're clearly overcounting here. Firstly, the order of each pair doesn't matter, so that's 2^4=16 times we're overcounting. Secondly, the order of the pairs doesn't matter, so that's 4!=24 times we're overcounting. Putting it all together, this gives 8!/(2^4*4!)=105. Another, simpler way to count (suggested to me by djedi) is that there are 7 choices to pair point 1 with. There are 5 choices to pair the next point with, 3 for the next and the last is determined, so that gives 7*5*3=105. Good to know!
Now the tricky part. I thought there was some nice way to count the symmetries, but I was thinking of Pólya counting, which is pretty neat but I couldn't see how to apply it. Not that I could remember this in Austin, so I used the Orbit-stabilizer theorem instead.
There are three types of symmetries a tile can had - 90 degree symmetry, 180 degree symmetry and no symmetry. Let's count how many tiles have each.
90 degree - a 90 degree rotation takes 1->3, 2->4, 3->5, 4->6, 5->7, 6->8, 7->1 and 8->1. So we have the chains 1->3->5->7 and 2->4->6->8. This gives the following tiles: (12)(34)(56)(78), (14)(36)(58)(72), (16)(38)(52)(74), (18)(32)(54)(76), (15)(37)(26)(48). It's surprisingly hard to find all these.
180 degree - here the chains are 1->5, 2->6, 3->7, and 4->8. If we list all these out, excluding the ones that have 90 degree symmetry, we get 10 tiles. (another mistake I made was counting 20 of these, but I was counting each rotation of each tile)
no symmetry - we'll count these by elimination, thank goodness.
So each 90 degree tile shows up once in the list of 105, each 180 degree tile shows up twice in the list of 105, and each tile with no symmetry shows up four times in the list of 105. So, there are (105-5-10*2)/4=20 distinct tiles with no symmetry. Adding, we get a total of 5+10+20=35 tiles, just like we wanted!!
Anyway, that's why the game is truly beautiful. We're going to game night at a game store tomorrow night and I'll see if they have a copy :-)
good times
Mood: happy
Posted on 2006-09-22 23:06:00
Tags: math
Words: 636
Things I'm happy about:
- We went to game night tonight and had a lot of fun. We played three games, all of which are guaranteed to terminate! Although the proof for the last one was a little tricky to come up with. Here are the rules:
You start with a stack of cards. There may also be cards in front of you, and cards on the table (that anyone can access). On your turn, you start one of two ways:
a) Drawing two cards from the stack
b) Drawing a set of cards from the table (not from in front of you).
Then, you do one of two things:
1) Play one card from your hand to the table (not in front of you)
2) Play a set of cards from your hand to in front of you.
If you started your turn with b), you must end it with 2), and you must play those cards you drew from the table to in front of you (along possibly with cards from your hand).
Given these rules, can you prove the game terminates? (the game terminates when the stack of cards is depleted, or some other condition that isn't relevant here)
So I first tried to show that the number of cards in the stack plus the total number of cards in everyone's hand must decrease on every turn (which means eventually the number of cards in the stack will go to 0, which ends the game). This, however, is not true: if you pick up cards from the table then play them in front of you (with no additions from your hand), that stays constant.
So, someone pointed out that the flow of cards is unidirectional: they always flow in the direction of
stack -> someone's hand -> table -> in front of someone
(sometimes they jump around, but they always go from left to right). So you can formalize this by showing that the sum
N^3*(number of cards in stack) + N^2*(total number of cards in everyone's hand) + N*(number of cards on table) + (total number of cards in front of someone)
is decreasing on every turn for sufficiently large N. It turns out that N=20 or so is sufficiently large, since that's the most number of cards that can be played in front of someone in one turn.
- djedi seems to be happy about work, which is nice. I'm excited about the project I'm working on.
- I've been going to the gym every other day, and lifting weights at my computer the other days (we've been playing a lot of WoW recently and it's convenient to do during downtime). I gained some weight last week mostly due to a batch of delicious brownies that I ate in like two days, but I'm back down to the previous weight already. (and I had two donuts for lunch on Thursday...and then I discovered "cookie time"!)
- We're going to the Maryland Renaissance Festival (weird that they picked the domain rennfest.com, although renfest.com was already taken: why not marylandrenfest.com or something?) tomorrow, which should be fun. The weather has nice (if a little chilly at times) so hopefully it'll be a beautiful day and not rain like my forecastfox is suggesting.
random: Last year a Japanese company had Sotheby's and Christie's compete for the right to sell their paintings by playing rock, paper, scissors. Christie's won by consulting teenage daughters of an executive, who came up with the correct strategy. Note that they got around the usual "on 3 or after 3?" question by having the combatants write down their choice on a sheet of paper. (via kottke via girlhacker)
I have the top Google Images result for her extra legs. Awesome!
Also, I've been extremely out at work and there haven't been any problems and I feel pretty good about that.
baseball series probabilities
Mood: curious and mathy
Posted on 2006-06-30 09:36:00
Tags: baseball math
Words: 790
So when Rice was in the NCAA baseball tournament and College World Series, I thought about how one baseball game or even a three-game series weren't really enough to determine which team was better, which is why MLB playoff series are 5 or 7 games, which certainly seems enough to tell for sure which team is better. Trying to figure out how true that was, I modeled it mathematically:
So, let's be formal here: the Astros are playing the Blue Jays, and the Astros have an x chance of beating the Blue Jays in any given game. (for 0 <= x <= 1) Assume that we have no prior knowledge of x - i.e. the probability of x is evenly distributed from 0 to 1. Given that the Astros beat the Blue Jays, what is the probability that x >= .5? (that is, the Astros are "better" than the Blue Jays)
Since the probability that the Astros beat the Blue Jays in one game is simply x, we're looking at the area under the curve y = x, which is of course the integral of x. So the probability that x >= .5 is just (the integral of x from .5 to 1)/(the integral of x from 0 to 1) = (1/2 - 1/8)/(1/2) = 3/4.
(hmm, this would look a lot nicer in LaTeX)
The nice thing about this method is that it easily generalizes - let's say that the Astros beat the Blue Jays two times. Since the probability that the Astros win both games is x^2, the probability that x >= .5 is (the integral of x^2 from .5 to 1)/(the integral of x^2 from 0 to 1) = (1/3 - 1/24)/(1/3) = 7/8.
And let's say the Astros beat the Blue Jays in a best out of 3 series. The probability that the Astros win the series is x^2 + 2*(1-x)*x^2 = 3*x^2 - 2*x^3, so the probability x >= .5 is (1/2 - 3/32)/(1/2) = 13/16, which is .8125. (which is less than 7/8, which smells wrong to me, but sort of makes sense because a best of 3 series always chooses a winner, while "winning 2 games" doesn't. Feel free to start checking my math at this point, though :-) )
If the Astros beat the Blue Jays in a best out of 5 series, the probability that the Astros win the series is x^3 + 3*(1-x)*x^3 + 6*(1-x)^2*x^3 = 10*x^3 - 15*x^4 + 6*x^5. So the probability that x >= .5 is (1/2 - 5/64)/(1/2) = 27/32, which is about .844.
Finally, for a best out of 7 series, the probability that the Astros win the series is x^4 + 4*(1-x)*x^4 + 10*(1-x)^2*x^4 + 20*(1-x)^3*x^4 = 35*x^4 - 84*x^5 + 70*x^6 - 20*x^7. So the probability that x >= .5 is (1/2 - 35/512)/(1/2) = 221/256, which is about .863.
# games in series Probability winner is "better" team
1 .75
3 .8125
5 .844
7 .863
So, this is all well and good, but the results seems a little unrealistic - I find it hard to believe that the best team wins 3 out of 4 times in just a single game. Let's try to remove some of the simplifying assumptions.
In the real world, the Astros beating the Blue Jays 100% of the time is just not going to happen. If we look at the final MLB standings from 2005, no team had a winning percentage below .3 or above .7, so let's try using .3 <= x <= .7 instead of 0 <= x <= 1. So we just have to recalculate all the integrals. This leads to the following results, assuming my math is correct (thanks to this numerical integrator):
# games in series Probability winner is "better" team
1 .6
3 .646
5 .678
7 .702
These probabilities seems a bit more realistic.
Finally, we've been assuming that x is distributed uniformly, but I'd say more teams are close in relative ability to each other. So let's try distributing x as a probability function over .3 to .7. We can use a "tent" function that peaks at .5 - something like 1 - 5 * abs(x-.5). (this hits the points (.3, 0), (.5, 1), and (.7, 1)). Again, this is relatively easy to calculate - we just multiply the expression we were integrating by (1 - 5 * abs(x - .5)). Doing this leads to our final results:
# games in series Probability winner is "better" team
1 .567
3 .598
5 .621
7 .639
So there you have it - under this model, even a 7 game series will only pick the better team 64% of the time. The probability function may have been a little too harsh here, so the 70% in table 2 might be a better guideline.
To make this more accurate, we should recognize that even if the Astros have an x chance of beating the Blue Jays, on any particular night the starting pitcher for both teams adds a bit of variance to that factor. This might be interesting to look at at some point.
Thanks for reading this far! Comments (especially pointing at mistakes) are most welcome.
This backup was done by LJBackup.