



Next: Fibonacci Numbers (last year)
Up: Basic Number Theory
Previous: Definitions
Contents
By definition of mod, 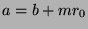 and
and 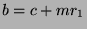 for some
for some
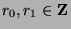 . So, by
substitution,
. So, by
substitution,  , and by the distributive property,
, and by the distributive property,
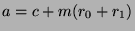 , so
, so
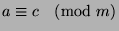 .
.
By definition of divides, 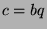 and
and 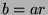 for some
for some  . Substituting, we find
that
. Substituting, we find
that 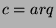 , so
, so  by the definition of divides.
by the definition of divides.
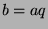 for some integer
for some integer 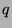 by definition of
by definition of 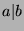 . Since
. Since  and
and 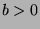 ,
then
,
then 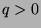 . If
. If 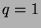 , then
, then 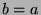 , so
, so 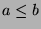 . Otherwise,
. Otherwise, 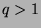 , so
, so 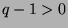 ,
so we can subtract
,
so we can subtract  and factor on the right to get
and factor on the right to get 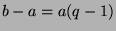 . Since
. Since
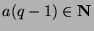 , then
, then 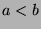 by definition, so
by definition, so 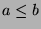 .
.
Fact 4
Let

and
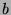
be integers, with
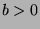
. Then there exist
unique integers q and r such that
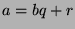
, where

. This is called
the division algorithm.
Let 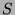 be the set of all numbers of the form
be the set of all numbers of the form 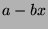 , where
, where 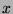 is an integer,
such that
is an integer,
such that 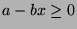 . If
. If  , then let
, then let  , so
, so 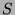 has an element.
If
has an element.
If  , then let
, then let  , so S has an element. If
, so S has an element. If 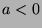 , then let
, then let  , so
, so
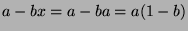 . Since
. Since 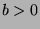 , then
, then 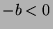 , so
, so 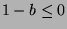 . If
. If 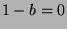 ,
then
,
then 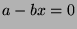 , so
, so 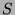 has an element. If
has an element. If 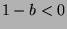 , then
, then 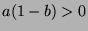 (since
(since 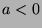 ), so
), so 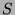 has an element. So,
has an element. So, 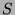 is not empty. Now, if
is not empty. Now, if
 , then
, then 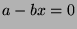 for some
for some 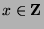 , and we can let
, and we can let 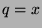 and
and  , so
, so
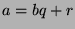 where
where  , so we are done. So, the other case we have to
consider is if
, so we are done. So, the other case we have to
consider is if 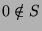 . Then
. Then
 , so by WOP, S has a least
element
, so by WOP, S has a least
element 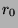 . Since
. Since 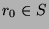 , we know that
, we know that 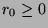 . So, we need to
show that
. So, we need to
show that 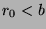 . Assume that
. Assume that 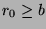 and try to arrive at a contradiction
(this is called proof by contradiction).
and try to arrive at a contradiction
(this is called proof by contradiction). 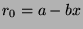 for some
for some 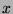 since
since
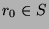 . Let
. Let 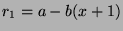 . So
. So
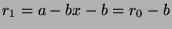 . Since
. Since 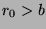 ,
,
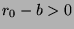 (by definition of
(by definition of 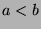 ). So
). So 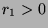 , and
, and 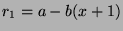 , so
, so
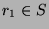 . But
. But 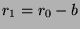 , so
, so 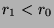 . However, this is not true,
since
. However, this is not true,
since 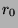 is the least element in
is the least element in 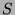 . So, we have arrived at a
contradiction, so our hypothesis was incorrect - so
. So, we have arrived at a
contradiction, so our hypothesis was incorrect - so 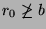 , so
, so
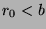 .
.
Fact 5
Let
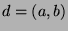
. Then there exist integers
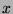
and
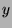
such that

.
Let 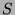 be the set of all numbers that can be expressed as
be the set of all numbers that can be expressed as 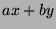 such that
such that
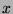 and
and 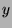 are integers and
are integers and 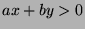 .
. 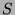 is not empty, since we can choose
is not empty, since we can choose
 and
and 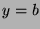 , so
, so 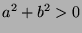 , so
, so 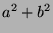 is in
is in 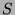 . Since
. Since 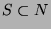 , by WOP
, by WOP 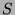 has a least element, which we will call
has a least element, which we will call 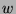 . If we can show
that
. If we can show
that 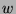 is the GCD of
is the GCD of  and
and 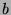 , then we will be done, because
, then we will be done, because 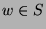 , so
, so
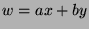 for some integers
for some integers 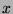 and
and 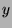 . Now we will show that
. Now we will show that 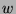 is the GCD
of
is the GCD
of  and
and 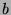 by using the definition of GCD.
by using the definition of GCD.
Part 1: WTS:  and
and  .
.
By the division algorithm, 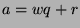 for some
for some 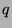 and
and 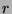 in
in  such that
such that  . We want to show that
. We want to show that  , so we will assume that
, so we will assume that
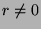 and try to reach a contradiction. Since
and try to reach a contradiction. Since 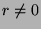 and
and  ,
we know that
,
we know that 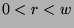 . We know
. We know  (since
(since 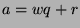 ). Since
). Since 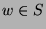 , we
can find an
, we
can find an 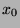 and a
and a 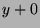 in
in  such that
such that 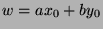 . We can
substitute in to get
. We can
substitute in to get
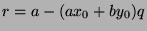 , or
, or
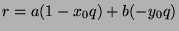 , which
means that
, which
means that  . But,
. But, 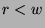 , and this contradicts the fact that
, and this contradicts the fact that 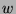 is the
least element in
is the
least element in 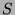 . So, we conclude that
. So, we conclude that  , so
, so 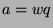 , so
, so  .
Similarly,
.
Similarly,  .
.
Part 2: WTS: If 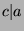 and
and 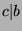 then
then 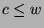 .
.
By definition of divides,  and
and  for some
for some 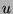 and
and  in
in
 . Since
. Since 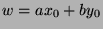 , we can substitute to get
, we can substitute to get 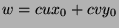 , so
, so
 , so
, so  (by definition of divides), so by Fact 1,
(by definition of divides), so by Fact 1, 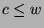 .
.
Fact 6
If there exist integers
,
such that
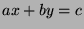
, then
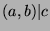
.
Let 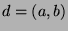 , so
, so 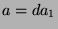 and
and 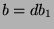 . So,
. So, 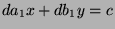 , so
, so
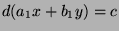 , so
, so 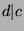 by definition of divides, so
by definition of divides, so 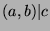 .
.
Since 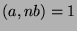 , there exist integers
, there exist integers 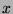 ,
, 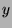 , such that
, such that 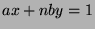 .
We can write this as
.
We can write this as 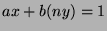 , so
, so 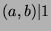 (by Fact 6), and
since
(by Fact 6), and
since 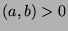 , then
, then 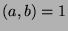 .
.
We know 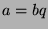 and
and  for some
for some  . Since
. Since 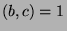 , then
, then
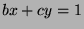 for some
for some 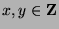 by Fact 5. We can multiply by
by Fact 5. We can multiply by  to get
to get 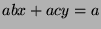 . We can substitute to get
. We can substitute to get 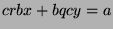 , and factor to get
, and factor to get
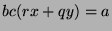 , so
, so 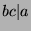 by definition of divides.
by definition of divides.
Since 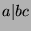 , we know
, we know 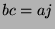 for some
for some 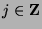 .
. 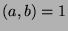 , so
, so 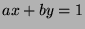 for
some
for
some 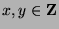 . Multiply by c to get
. Multiply by c to get 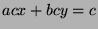 , substitute to get
, substitute to get
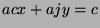 , and factor to get
, and factor to get 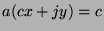 . So, by definition of divides,
. So, by definition of divides,
 .
.
There exist integers 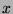 ,
, 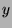 such that
such that 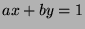 by Fact 5, so
by Fact 5, so
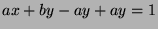 , so
, so 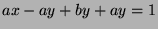 , so
, so
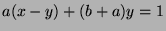 , so
, so 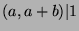 (by Fact 6), so
(by Fact 6), so  .
.
We will prove this by contradiction. Assume for the sake of contradiction that
there exists a 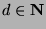 such that
such that  and
and 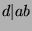 and
and 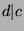 . Now, assume for
the sake of contradiction that
. Now, assume for
the sake of contradiction that 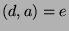 , where
, where 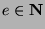 and
and 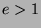 . Then
. Then
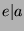 and
and 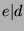 . Since
. Since 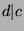 , by Fact 2 we can say that
, by Fact 2 we can say that
 . So, since
. So, since 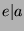 and
and  and
and 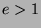 , this is a contradiction to
, this is a contradiction to
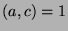 , and we conclude that
, and we conclude that 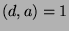 . Now, since
. Now, since 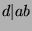 , by Fact
9,
, by Fact
9, 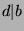 . But, since we know that
. But, since we know that 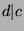 , this is a contradiction to
, this is a contradiction to
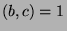 . So,
. So, 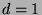 , and we conclude that
, and we conclude that  .
.
This will be proven by weak mathematical induction on 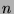 .
.
Base Case: Want To Show(WTS): 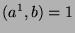 .
.
Since  and
and 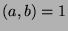 , then
, then 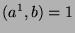 .
.
Induction Step: Assume 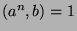 .
.
WTS:  .
.
Since we know that 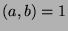 and
and 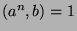 , we can apply Fact
11 to say that
, we can apply Fact
11 to say that 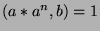 , or
, or  .
.
Fact 13
If
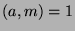
, then there exists some
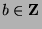
such that
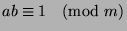
.
There exists 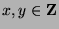 such that
such that 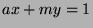 (by Fact 5), so
(by Fact 5), so
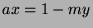 , so
, so
 .
. 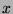 is the integer we were looking for, so
we are done.
is the integer we were looking for, so
we are done.
By definition of mod,  , and since
, and since 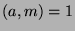 , then
, then 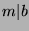 (by Fact
9), so
(by Fact
9), so
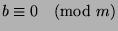 , and we are done.
, and we are done.
Since 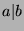 , then
, then 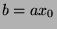 for some
for some 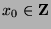 . Since
. Since 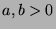 , then
, then 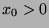 .
Since
.
Since 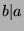 , then
, then 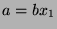 for some
for some 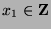 . Since
. Since 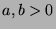 , then
, then 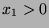 .
Substituting, we find that
.
Substituting, we find that  , or
, or 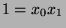 . Since
. Since  , it
follows that
, it
follows that 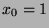 and
and  . Substituting, we find that
. Substituting, we find that 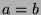 .
.
Since
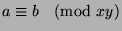 , then
, then 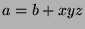 , for some
, for some 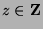 . So,
. So,
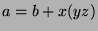 , so
, so
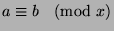 by definition of mod.
by definition of mod.




Next: Fibonacci Numbers (last year)
Up: Basic Number Theory
Previous: Definitions
Contents
Gregory Stoll
2000-04-08
![]() and
and ![]() .
.
![]() for some
for some ![]() and
and ![]() in
in ![]() such that
such that ![]() . We want to show that
. We want to show that ![]() , so we will assume that
, so we will assume that
![]() and try to reach a contradiction. Since
and try to reach a contradiction. Since ![]() and
and ![]() ,
we know that
,
we know that ![]() . We know
. We know ![]() (since
(since ![]() ). Since
). Since ![]() , we
can find an
, we
can find an ![]() and a
and a ![]() in
in ![]() such that
such that ![]() . We can
substitute in to get
. We can
substitute in to get
![]() , or
, or
![]() , which
means that
, which
means that ![]() . But,
. But, ![]() , and this contradicts the fact that
, and this contradicts the fact that ![]() is the
least element in
is the
least element in ![]() . So, we conclude that
. So, we conclude that ![]() , so
, so ![]() , so
, so ![]() .
Similarly,
.
Similarly, ![]() .
.
![]() and
and ![]() then
then ![]() .
.
![]() and
and ![]() for some
for some ![]() and
and ![]() in
in
![]() . Since
. Since ![]() , we can substitute to get
, we can substitute to get ![]() , so
, so
![]() , so
, so ![]() (by definition of divides), so by Fact 1,
(by definition of divides), so by Fact 1, ![]() .
.
![]() .
.
![]() and
and ![]() , then
, then ![]() .
.
![]() .
.
![]() .
.
![]() and
and ![]() , we can apply Fact
11 to say that
, we can apply Fact
11 to say that ![]() , or
, or ![]() .
.