World Cup: Advancing out of the Group Stage
About this project: After the USA was drawn into the "group of death" in 2014 (with Germany, Portgual, and Ghana), I wondered how many points it would take to get out of the group stage.
The way the group stage works is: four teams, each plays each other one time, wins are worth 3 points, draws are worth 1 point. The top two teams advance.
To simplify things I just assumed every game had an equal probability of drawing or either team winning. For tiebreakers, I assumed a uniform distribution of who gets to go on. So, without further adieu:
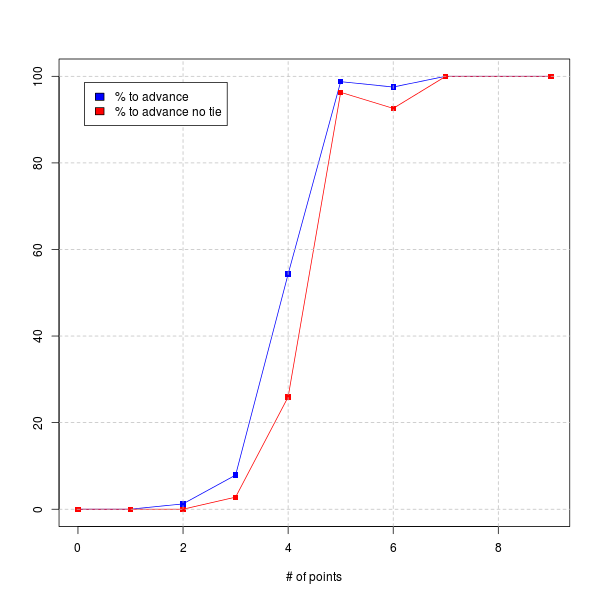
| # points | % to advance | % advance without tiebreaker |
|---|---|---|
| 0 | 0.00% | 0.00% |
| 1 | 0.00% | 0.00% |
| 2 | 1.23% | 0.00% |
| 3 | 7.87% | 2.78% |
| 4 | 54.32% | 25.93% |
| 5 | 98.77% | 96.30% |
| 6 | 97.53% | 92.59% |
| 7 | 100.00% | 100.00% |
| 8 | - | - |
| 9 | 100.00% | 100.00% |
Observations:
- There's a huge jump between 3 and 4 points and 4 and 5 points. 4 points is kind of average (one win, one draw, and one loss), so it makes sense that you have around a 50-50 chance of advancing.
- There's also a weird tiny dip between 5 and 6 points, probably because if you have 5 points you know there are two draws, which lowers the total amount of available points to other teams in the group.
- Also, even if you only get two points you're not mathematically eliminated!
Some other group probabilities
Someone wrote in asking how likely it was for a group to finish in some interesting ways. Again, this assumes every game has an equal probability of drawing or either team winning:
All four teams getting 3 draws
There are six games in the group stage, and the probability of a draw is 1/3, so the probability of all six games being draws is (1/3)^6 = 1/729, or about 0.14%.
One team getting 9 points, one team getting 6 points, one team getting 3 points, one team getting 0 points
First we have to pick which team will finish first, second, third, and last: there are 4! = 24 ways to do that. Now that we know that, each match has to end with the higher ranked team defeating the lower ranked team, so like the previous scenario, there's a 1/729 chance of that. So the overall chance is 24/729, or about 3.3%.
All teams getting one win, one draw, and one loss
Hmm, this is trickier. Let's say the teams are A, B, C, and D. First we have to choose which teams are going to draw with each other; this can be either A/B and C/D, A/C and B/D, or A/D, and B/C, so there are 3 choices. Then for the other 4 games, there must be a cycle; let's say we're in the A/B and C/D draw scenario, there are only two possible series of games. Either A beats C beats B beats D beats A, or A beats D beats B beats C beats A. So there are 3*2=6 determinations of how all the group stage games have to work out, and the overall chance is 6/729, or about 0.82%.
Source files:
- worldCupSimulator.py - the Python script that generated these. Code is very hacky because I wrote it quickly. It just enumerates all 3^6 possibilities and tallies them up.
- rplotscript.txt - script to generate the graph