



Next: Theorems
Up: Fibonacci-q numbers and new
Previous: Fibonacci-q numbers and new
Contents
- The Fibonacci-
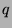 sequence (the
sequence (the 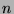 th term of which is denoted
th term of which is denoted 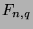 )
is defined recursively by the following statements:
Note that the regular Fibonacci numbers can be denoted by
)
is defined recursively by the following statements:
Note that the regular Fibonacci numbers can be denoted by 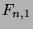 in this notaion.
in this notaion.
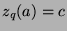 means that
means that  has the following properties:
has the following properties:
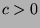 .
.
-
 .
.
 is the least positive integer satisfying these properties.
is the least positive integer satisfying these properties.
 means that
means that 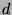 has the following properties:
has the following properties:
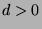 .
.
-
 .
.
-
 .
.
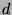 is the least positive integer satisfying these properties.
is the least positive integer satisfying these properties.
Note: 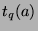 is then the function that gives the period of the Fibonacci-
is then the function that gives the period of the Fibonacci-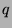 sequence in modulo
sequence in modulo  .
.
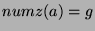 means that
means that 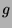 has the following properties:
has the following properties:
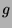 is the number of
is the number of 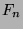 that are congruent to
that are congruent to 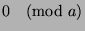 , where
, where 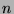 goes from
goes from
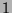 to
to 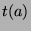 , inclusive.
, inclusive.
-
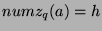 means that
means that 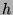 has the following properties:
has the following properties:
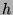 is the number of
is the number of 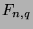 that are congruent to
that are congruent to 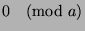 , where
, where 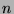 goes from
goes from
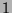 to
to 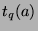 , inclusive.
, inclusive.
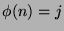 (known as the Euler phi function) means that
(known as the Euler phi function) means that 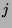 has the following
properties:
has the following
properties:
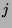 is the number of
is the number of 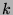 such that
such that 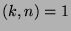 , where
, where 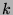 goes from
goes from 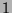 to
to 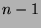 ,
inclusive.
,
inclusive.




Next: Theorems
Up: Fibonacci-q numbers and new
Previous: Fibonacci-q numbers and new
Contents
Gregory Stoll
2000-04-08
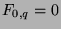 .
.
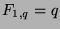 .
.
 ,
, 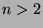 .
.
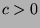 .
.
 .
.
 is the least positive integer satisfying these properties.
is the least positive integer satisfying these properties.
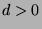 .
.
 .
.
 .
.
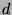 is the least positive integer satisfying these properties.
is the least positive integer satisfying these properties.
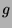 is the number of
is the number of 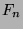 that are congruent to
that are congruent to 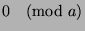 , where
, where 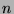 goes from
goes from
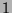 to
to 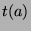 , inclusive.
, inclusive.
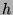 is the number of
is the number of 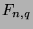 that are congruent to
that are congruent to 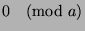 , where
, where 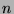 goes from
goes from
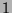 to
to 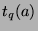 , inclusive.
, inclusive.
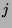 is the number of
is the number of 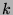 such that
such that 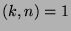 , where
, where 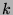 goes from
goes from 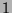 to
to 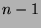 ,
inclusive.
,
inclusive.